Auteur : avialatoux

Guidage linéaire

| avialatoux

Il existe différent moyen de faire un guidage en translation. Les plus couramment utilisés de nos jours, sont les suivants :

Guidage par arbre cannelé :

arbre cannelé

Ils sont surtout utilisés pour de faibles déplacements à faible vitesse.

Il y a deux façon de monter un arbre cannelé :

arbre cannelé montage

Guidage par clavetage libre :

clavetage libre

Ils sont surtout utilisés pour de faibles déplacements à faible vitesse.

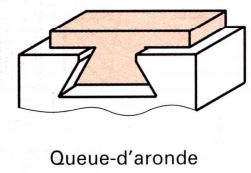
Guidage par queue d’aronde :

queue d'aronde

Ils sont surtout utilisés pour de faibles déplacements à faible vitesse. Ce système est de moins en moins utilisé.

Guidage par rainure en T :

guidage rainure en T

Ce système de guidage est surtout utilisé pour réaliser un système de bridage après avoir guidé en translation la pièce pour la positionner. Il est utilisé pour de faibles déplacements à faible vitesse.

Guidage par double tige :

guidage double tige

Ce système de guidage est utilisé pour des grands déplacements à vitesse élevée.

Guidage par roulement :

Il existe deux grands types de guidage par roulement, avec rail de guidage et avec douille à billes.

  • Rail de guidage :

rail de guidage

Les guidages linéaires sur patins sont utilisés dans la mécanique de précision (automation, dispositifs de contrôle et de mesure…).

Ils permettent une absence totale de jeu et ils possèdent un très faible coefficient de frottement (0,0005 à 0,003). Vitesse de déplacement de 3 à 5 m/s

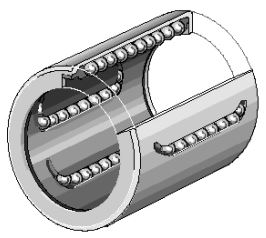
  • Douille à billes :

douille à billes

Elles permettent des fonctionnements sans jeux, améliorent la précision et les performances. La valeur du coefficient de frottement varie de 0,001 à 0,005.

Elles se montent par paire et sont utilisées sur les machines-outils, robots, systèmes automatisés…

Vitesse de déplacement 5 m/s.

Elles sont économiques pour arbres lisses et ne supportent que des charges radiales.

Calcul de rotation

| avialatoux

rotation

Vous connaissez les coordonnées du point A et du point B ainsi que l’angle de rotation voulu, trouver le point B’ sera un jeu d’enfant grâce à la formule matricielle suivante :

rotation formule

NB :

La formule matriciel suivante est valable uniquement si la rotation se fait dans un plan.

On tourne toujours en sens trigonométrique sinon il faut multiplier le résultat par -1.

Le 1 qui apparaît dans les matrices 3,1 ne correspond absolument pas à la coordonnée en z du point.

Exemple :

A(2;3)                    B(5;10)                           φ= π

 rotation exemple

Quelques lois de résistance des matériaux

| avialatoux

Hypothèses de la RDM :

  • Le matériau est homogène et isotrope
  • Les pièces sont assimilables à des poutres
  • Les actions mécaniques sont comprises dans le plan de symétrie de la poutre ou sont symétriques par rapport à celui-ci
  • Les déformations sont faibles donc on suppose que les points d’application des forces ne bougent pas après déformation.

Torseur de cohésion d’une poutre :

rdm

Traction – compression :

σ = N/S

σ = E*a

Avec :

N : effort normal en Newton

S : surface de la section en m²

E : module de Young en Pa

a = Δl/l : allongement relatif

σ : contrainte normale

Il ne reste plus qu’à comparer σ avec σe (contrainte limite de comportement élastique) et σr (contrainte de rupture) ainsi que les contraintes du cahier des charges

Cisaillement :
τ = T/S

τ = G*γ

Avec :

T : effort tranchant en Newton

S : surface de la section en m²

G : module de Coulomb en Pa

γ = Δy/Δx : glissement transversal relatif

τ : contrainte tangentielle

Il ne reste plus qu’à  comparer τ avec τe (contrainte limite de comportement élastique) et τr (contrainte de rupture) ainsi que les contraintes du cahier des charges

Torsion :

Torsion

Les moments quadratiques de différents profilés sont donnés par les différents fournisseurs.

τ = d*Mt/IG

Mt = G*θ*IG

Avec :

Mt : moment de torsion en Nm

d : distance au centre de la section (distance la plus éloignée du centre de préférence)

IG : moment quadratique polaire de la section en m4

G : module de Coulomb en Pa

θ = α/x : angle de torsion unitaire en rad/m

Il ne reste plus qu’à  comparer τ avec τe (contrainte limite de comportement élastique) et τr (contrainte de rupture) ainsi que les contraintes du cahier des charges

Flexion :

flexion

Les moments quadratiques de différents profilés sont donnés par les différents fournisseurs.

Les formules sont faites à partir de la configuration suivante :

flexion 2

σ = -y*Mfz/IGz

Mfz = E*f »*IGz

Avec :

Mfz : moment de flexion en Nm

IGz : moment quadratique de la section par rapport à l’axe (Gz) en m4

y : distance par rapport à l’axe (Gz) en m

E : module de Young en Pa

f : flèche (écart verticale par rapport à la position sans sollicitation) en m

f » : dérivée seconde de la flèche par rapport à l’abscisse x

Pour obtenir l’expression de la flèche, on intègre deux fois la formule précédente. Les constantes qui apparaissent lors des intégrations sont déterminées grâce aux conditions limites.

Il ne reste plus qu’à comparer σ avec σe (contrainte limite de comportement élastique) et σr (contrainte de rupture) ainsi que les contraintes du cahier des charges

Ajustement

| avialatoux

Les ajustements les plus utilisés pour les assemblages mécaniques sont de différents type et ils ont tous leurs propres caractéristiques.

Ajustement avec jeu moyen :

Nom : H8f7

On l’utilise pour les guidages tournant ou glissant avec jeu, il permet aussi un bon graissage.

Ajustement avec jeu faible :

Nom : H7g6

Cet ajustement est principalement utilisé pour réaliser un guidage (tournant ou glissant) précis.

Ajusté :

Nom : H7h6 ou H8h7

On utilise cet ajustement pour un centrage ou un positionnement. Le montage peut se faire à la main, cependant on ne peut pas transmettre d’efforts entre ces deux pièces. Il n’y aura pas de détériorations des pièces au démontage.

Ajustement peu serré :

Nom : H7m6

On utilise cet ajustement pour avoir un centrage ou un positionnement de meilleure qualité que le précédent. Le montage doit se faire à la masse et il ne peut pas transmettre d’efforts. Il n’y aura pas de détériorations au démontage.

Ajustement serré :

Nom : H7p6

Cet ajustement est utilisé pour transmettre les efforts, après le montage, à la presse, les deux pièces ne font plus qu’une. Si on démonte les pièces, on devra les réusiner pour les réutiliser.

alésage tolérence

arbre tolérence

Les ressorts

| avialatoux

Un ressort est un élément mécanique qui peut revenir à son état initial après avoir subi une déformation relativement importante.

SpringA1

Pour dimensionner un ressort, il faut bien suivre les étapes qui vont suivre.

1- Calcul de d mini :

d mini

Avec :

F : force maxi de résistance du ressort en N

G : module de Coulomb

w doit être fixé. La norme accepte des valeurs comprises entre 4 et 20 mais en pratique :

  • w=6 est la limite minimale (ressort très épais)
  • w=10 est la valeur courante pour obtenir un ressort équilibré et facile à fabriquer
  • w=16 est la limite supérieure (ressort très fin)

La valeur de d trouvée est la valeur minimale théorique. Il faut prendre la valeur acceptable la plus proche chez le fournisseur de fil dans le tableau des diamètres usuels ci-dessous :

d usuel

2- Calcul du diamètre extérieur De et du diamètre moyen D : 
D choisi
3- Calcul des valeurs manquantes :

Pour le calcul de L0, il faut fixer le type l’extrémité du ressort : ni = 1.5 pour les extrémités rapprochées et meulées et ni = 3 pour les extrémités rapprochées.

n : nombre de spires utiles

Les derniers calculs peuvent être définis selon plusieurs options.

Option 1 : la raideur R est imposée :

n avec R connu

L0

Option 2 : la longueur L0 est imposée :

L0 imposée

Option 3 : la déformation totale f est imposée :

n avec f connu

L0

Option 4 : rien n’est imposé :

On prend n=2 pour avoir le ressort le plus court possible. En effet, selon les normes de calcul, n ≤ 2

L0

4- Besoin du pas du ressort p?

pas ressort

Maintenant il ne vous reste plus qu’à commander votre ressort.

Calcul de volumes et de surfaces usuels

| avialatoux

L : longueur
l : largeur
b : petite base
B : grande base ou base du triangle
h : hauteur
R : rayon
P : profondeur
n : nombre de coté
c : coté

Surface Volume
Rectangle/Parallélépipède L*l  L*l*P
Trapèze/Parallélépipède  0.5(B+b)h 0.5(B+b)hP
Triangle/Parallélépipède 0.5Bh 0.5BhP
Disque/Cylindre πR2 PπR2
Parallélogramme/Parallélépipède Lh LhP
Polygone régulier/Paralélépipède 0.5nch  0.5nchP
Contour cylindre/Cylindre 2πRL  PπR2
Contour cône /Cône πR√(R2+h2) πhR2/3
Sphère 4πR2 4πR3/3

Rondelles

| avialatoux

Il existe toutes sortes de rondelles. Les plus utilisées sont répertoriées dans cet article.

Rondelle Belleville :

Les rondelles Belleville sont des ressorts coniques chargés axialement. Elles permettent de réaliser des ressorts peu encombrants sous de fortes charges ainsi qu’un très bon frein d’écrou. Suivant le but recherché, on les utilises :

  • Seules
  • Empilées dans le même sens (ce montage réalise l’addition des charges élémentaires)
  • Empilées en sens contraire (ce montage réalise l’addition des flèches élémentaires)
  • En montage mixte (on obtient à la fois l’addition des charges et des flèches élémentaires)

La course de travail d’une rondelle Belleville doit être au maximum égale aux trois quarts de la course.

La force axiale d’une rondelle Belleville est sensiblement proportionnelle à la course.

rondelle-ressort-dynamique-din-2093-acier-brut-71300-dmod1

Diamètre d1 (mm) Diamètre d2 (mm) Épaisseur s (mm) Charge (N)
 8 20 0.8 750
 10 25 0.9 950
 12 31.5 1.2 1600
 14  35 1.8 4000
 16  40 2 5300
 18  45 2.5 9500
 20  50 2 4800
25  50 2.5 9000
30  63 3 12000
40  83 4 23000
50  100 5 37000
 60  125 6 53000

Les rondelles à dents :

Le freinage est obtenu grâce à l’élasticité des dents. L’efficacité de ce freinage est augmentée du fait de l’incrustation des arêtes dans les pièces à freiner.

Ces rondelles permettent d’obtenir un très bon freinage et de contacts électriques très convenables. Il en existe 4 sortes :

  • Les rondelles à denture extérieure sont utilisées normalement avec un écrou ou une vis hexagonale
  • Les rondelles à denture intérieure sont utilisées avec un écrou (ou une vis) à surplat réduit ou si la surface de la pièce est irrégulière ou encore si l’on recherche une bonne esthétique.
  • Les rondelles à double denture conviennent particulièrement pour les assemblages comportant des trous de passage oblongs ou de diamètre beaucoup plus grands que ceux des vis utilisées.
  • Les rondelles à forme concave permettent le freinage des vis à tête fraisée.

rondelle à dents

Diamètre vis (mm) Diamètre intérieure (mm) Diamètre extérieur denture simple (mm) Diamètre extérieur denture double (mm) Diamètre extérieur forme concave (mm)
5 5.2 9.5 17.5 10
 6  6.2 11 18.5 12
 8  8.3 14 23 16
 10  10.3 17.5 26 19
 12  12.4 21 30 24
 14  14.5 24 33
 16  16.5 27 36
 18  18.5 30
 20  20.5 33
 22  22.8 37
 24  24.8 39
 27  27.8 44
 30  30.8 48

Les rondelles grower :

Le freinage est obtenu grâce à l’élasticité de la rondelle. L’efficacité de ce freinage est augmentée du fait de l’incrustation des bords relevés dans l’écrou (ou la tête de la vis) et dans la pièce.

rondelle-grower-serie-courante-w-nfe-25515-acier-brut-71000-dmod1

Diamètre d1 (mm) Diamètre d2 (mm) Épaisseur s (mm)
 3 5.4 1
4 7.5 1.5
5 8.5 1.5
6 10.6 2
8 14 2.5
10 17 3
12 21 3.5
14 24 4
16 26 4
18 30 5
20 32 5
22 34 5
24 38 6
27 42 6
30 47 7
33 50 7
36 55 8
39 58 8

Les rondelles plates :

Rondelle plate

Diamètre d1 (mm) Diamètre d2 (mm)
Série étroite (Z) Série moyenne (M) Série large (L) Série très large (LL)
2.5 5 7 10 12
3 6 8 12 14
4 8 10 14 16
5 10 12 16 20
6 12 14 18 24
8 16 18 22 30
10 20 22 27 36
12 24 27 32 40
14 27 30 36 45
16 30 32 40 50
18 32 36 45 55
20 36 40 50 60
22 40 45 55 65
24 45 50 60 70
27 48 55 65 75
30 52 60 70 80
33 65 75 85
36 70 80 90

Les plastiques usuels

| avialatoux

Il existe 9 principaux polymères utilisés en usinage, le polyéthylène, le polyamide 6-6 ou nylon, le POM C, le PVC, le téflon, le polycarbonate, le polyétheréthercétone, l’acrylonitrile butadiène styrène et le polyméthacrylate de méthyle.

Le PE : Polyéthylène

Atouts :

  • Prix
  • Faible coefficient de frottement (0.29)

Inconvénient :

  • Faibles propriétés mécaniques

module de Young : E = 1.2 GPa

coefficient de Poisson : v = 0.46

température d’utilisation  : entre -150 et 80°C

densité : 960 kg/m3

Le PA66 : Nylon

Atouts :

  • Faible coefficient de frottement (entre 0.2 et 0.3)
  • Bonnes propriétés mécaniques

module de Young : E = 3 GPa

coefficient de Poisson : v = 0.39

température d’utilisation  : entre -30 et 80°C

densité : 1140 kg/m3

Inconvénients :

  • Difficile à usiner

Le POM C :

Atouts :

  • Belle finition
  • Faible coefficient de frottement (entre 0.25 et 0.35)
  • Bonnes propriétés mécaniques

module de Young : E = 3 GPa

coefficient de Poisson : v = 0.35

température d’utilisation  : entre -50 et 95°C

densité : 1410 kg/m3

Inconvénients :

  • Légèrement plus chère que le PA66

Le PVC :

Atouts :

  • Bonne usinabilité
  • Bonnes propriétés mécaniques

module de Young : E = 4.14 GPa

coefficient de Poisson : v = 0.41

température d’utilisation  : entre -20 et 60°C

densité : 1400 kg/m3

Inconvénients :

  • Cassant

Le PTFE : Téflon

Atouts :

  • Résistance aux produits chimiques et à une température élevé (250 à 260°C)
  • Faible coefficient de frottement (0.1)

Inconvénients :

  • Prix
  • Faibles propriétés mécaniques

module de Young : E = 0.552 GPa

coefficient de Poisson : v = 0.46

température d’utilisation  : entre -200 et 260°C

densité : 2200 kg/m3

Le PC : Polycarbonate

Atouts :

  • Transparence

Inconvénients :

  • Difficile à usiner
  • Cassant
  • Fragile

module de Young : E = 2.44 GPa

coefficient de Poisson : v = 0.4

température d’utilisation  : entre -60 et 80°C

densité : 1200 kg/m3

Le PEEK : Polyétheréthercétone

Atouts :

  • Bonnes propriétés mécaniques

module de Young : E = 3.95 GPa

coefficient de Poisson : v = 0.39

température d’utilisation  : entre -80 et 260°C

densité : 1310 kg/m3

Inconvénients :

  • Prix

L’ABS : Acrylonitrile butadiène styrène

module de Young : E = 2.9 GPa

coefficient de Poisson : v = 0.422

température d’utilisation  : entre -30 et 80°C

densité : 1100 kg/m3

Le PMMA : Polyméthacrylate de méthyle

Atouts :

  • Transparence

Inconvénients :

  • Fragile

module de Young : E = 3.8 GPa

coefficient de Poisson : v = 0.4

température d’utilisation  : entre -40 et 80°C

densité : 1190 kg/m3

Filetages UNC

| avialatoux

Il s’agit des filetages UNC les plus utilisés pour les assemblages mécaniques.

UNC Diamètre extérieur (mm) Pas (mm) Diamètre de perçage (mm)
Nr. 4-40 UNC 2.845 0.635 2.3
Nr. 5-40 UNC 3.175 0.635 2.6
Nr. 6-32 UNC 3.505 0.794 2.7
Nr. 8-32 UNC 4.166 0.794 3.5
Nr. 10-24 UNC 4.826 1.058 3.8
Nr. 12-24 UNC 5.486 1.058 4.5
1/4 -20 UNC 6.350 1.270 5.1
5/16 -18 UNC 7.938 1.411 6.5
3/8 -16 UNC 9.525 1.588 7.9
7/16 -14 UNC 11.112 1.814 9.3
1/2 -13 UNC 12.700 1.954 10.7
9/16 -12 UNC 14.288 2.117 12.3
5/8 -11 UNC 15.875 2.309 13.5
3/4 -10 UNC 19.050 2.540 16.5
7/8 -9 UNC 22.225 2.822 19.3
1 -8 UNC 25.400 3.175 22.25